To solve problems like Two Sums, Product Except Self, or Contains Duplicate we have to access multiple values at the same time from a sequential data structure (for example, a Linked List or an Array).

The initial instinct while solving these problems is to use nested loops where each layer of the loop will maintain a different iterator on the data structure. But this approach does not scale well with the size of input as a single order of nested loops has $O(n^2)$ worst-case time complexity.

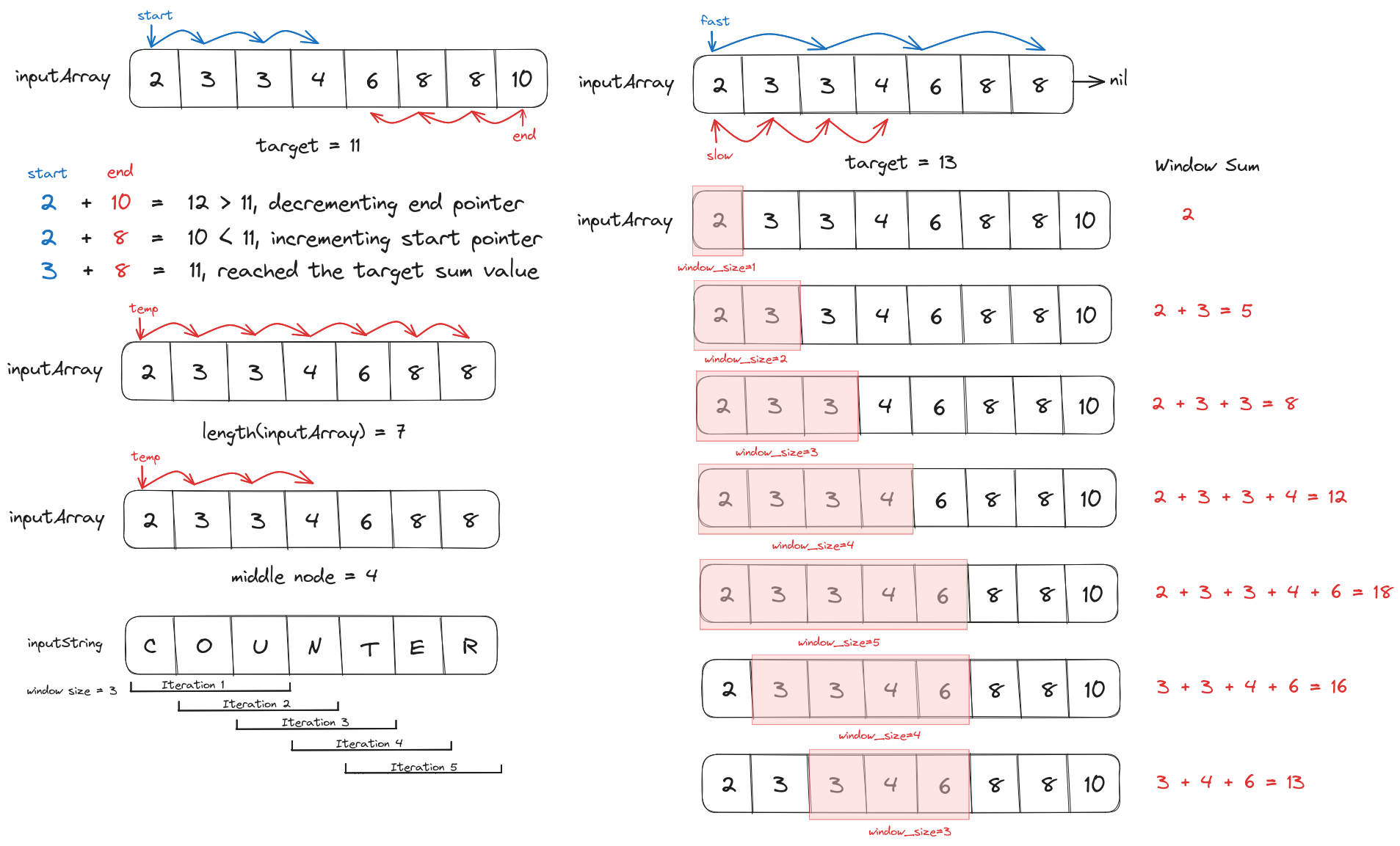
To implement a scalable solution we have to avoid nesting and access multiple values in a single loop by maintaining two iterators. We can use this two-pointer approach to solve the Two Sums problem (assuming the input is sorted).

startPointer = 0
endPointer = length(array)-1

while(startPointer<endPointer){
  sumValue = array
  if(sumValue==target){
    return (startPointer, endPointer)
  }
  else if (sumValue<target){

    // Since the sumValue is small we have
    // to increment the startPointer to a 
    // larger value
    startPointer += 1

  } else {

    // Since the sumValue is larger we have
    // to decrement the endPointer to a 
    // smaller value
    endPointer -= 1

  }
}

return none, none

Unlike the brute-force solution to two sums problem which uses nested loops to return results in quadratic time ($O(n^2)$), this approach will return results in linear time ($O(1)$) while also maintaining a constant space complexity.

Fast-Slow Pointers

The pointers can also iterate the data structure at an independent pace. For example, a fast pointer can iterate over two or more values at a time whereas a slow pointer can iterate over a single value at a time.

Finding the middle node of a Linked List

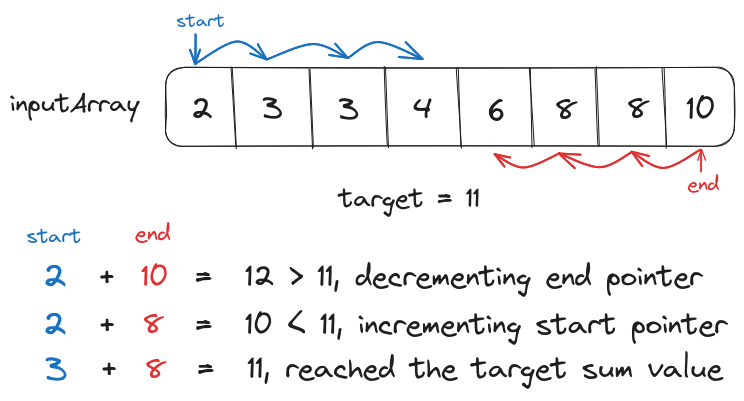
Assume that we have to find the middle node of a Linked List. The Linked List is a dynamically allocated data structure so its size could not be determined without iterating it once completely. So a loop with $O(n)$ time complexity will be executed on the linked list to determine its length $n$, then a second loop with $O(n/2)$ time complexity will be executed to fetch the middle node. This will result in the total time complexity of $O(n) + O(n/2)$ in the worst-case scenario.

// Finding the length of the linked list
linked_list_length = 1
temp = linked_list.head
while(temp.next != nil){
 temp = temp.next 
 linked_list_length += 1
}

// Iterating over the linked list until
// the middle node
middle_node_location = linked_list_length/2 
temp = linked_list.head
i=0
while(i<middle_node_location){
  temp=temp.next
  i+=1
}

return temp

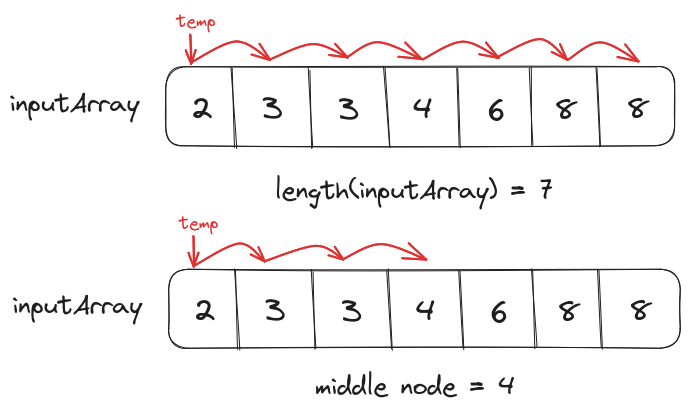
But we can reduce the time complexity of the solution to just $O(n)$ if we use a fast and a slow pointer to iterate over the linked list simultaneously. The slow pointer will iterate over every node in the linked list whereas the fast pointer will skip over every other node.

fast = linked_list.head
slow = linked_list.head

while(fast!=nil) or (fast.next!=nil){
  // fast will skip over every other node
  fast = fast.next.next

  // slow will iterate the linked list
  // one node at a time
  slow = slow.next
}

return slow

Since the fast pointer covers twice the distance as the slow pointer in the same number of iterations when it reaches the end of the linked list the slow pointer would be at the middle node.

Sliding Window

Some problems require analysis of sub-sequences of a data structure. Instead of iterating the data structure one value at a time, we can define a window and move it by one value on every iteration i.e. value/pattern identified from the previous window would be reused with the new element to analyze the current window, eliminating redundancy.

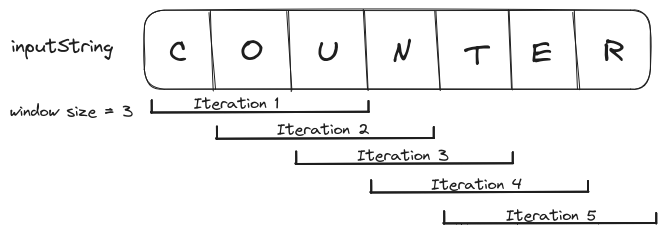
Depending on the problem, the window size could be static (constant on every iteration) or dynamic (variable on every iteration).

Static Window Size

If the subsequence size defined in the problem is static then the sliding window size will also be constant.

Calculating Moving Average

The Moving Average / Rolling Mean is the mean calculated over a window of values with a constant size.

For example, 30 days moving average, 5 months moving average, etc.

$$Mean(a_1, a_2, a_3, a_4, a_5)={(a_1+a_2+a_3+a_4+a_5) \over 5}$$ $$Mean_{Rolling}(a_1, a_2, a_3, \dots , a_n, 3)=Mean(a_1, a_2, a_3),\ Mean(a_2, a_3, a_4),\newline Mean(a_3, a_4, a_5),\ \dots,\ Mean(a_{n-2}, a_{n-1}, a_{n})$$

If we have to calculate the moving average of values over the data provided in the form of an array. We can implement a brute force solution that will use a nested loop of window size $k$ and calculate the individual averages.

func calculate_moving_average(array, k)
  moving_averages = []

  for index in array
    moving_sum = 0

    for index2 in range(0, k)
      // Calculating the sum of the current window
      moving_sum += array[index+index2]

    // Appending the average from the current window 
    // to the moving average list 
    moving_averages.append(moving_sum/k)
  
  return moving_averages

This approach will result in the total time complexity of $O(kn)$ where $k$ is the size of the window and $n$ is the number of elements in the array.

By using a sliding window of size $k$ (the moving average window size) we can eliminate the nested loop from the solution and decrease the total time complexity to $O(n)$.

We know the formula for calculating the mean over the window of the first 3 values is $$Mean(a_1, a_2, a_3)={(a_1+a_2+a_3) \over 3}$$

Instead of calculating the next rolling mean from scratch, we can use the value of $Mean(a_1, a_2, a_3)$ by adding the value of the element introduced in this window and subtracting the value of the element from the previous window (divided by the window size).

$$Mean(a_2, a_3, a_4) = {{a_2 + a_3 + a_4} \over 3}$$ $$Mean(a_2, a_3, a_4) = {{a_2 + a_3 + a_4 + a_1 - a_1} \over 3}$$ $$Mean(a_2, a_3, a_4) = {{a_1 + a_2 + a_3} \over 3} + {a_4 \over 3} - {a_1 \over 3}$$ $$Mean(a_2, a_3, a_4) = {{a_1 + a_2 + a_3} \over 3} + {{a_4 - a_1} \over 3}$$ $$Mean(a_2, a_3, a_4) = Mean(a_1, a_2, a_3) + {{a_4 - a_1} \over 3}$$

func average(values)
  return sum(values)/length(values)

func calculate_moving_average(array, k)
  moving_averages = []

  // Calculating the average value of the 
  // first window
  temp_average = average(array[:k])
  moving_averages.append(temp_average)

  for index in range(k, length(array))

    // Using the average value from the 
    // previous window to calculate the average 
    // value of the current window
    temp_average = temp_average + (array[index] + array[index-k])/k
    moving_averages.append(temp_average)
  
  return moving_averages

Dynamic Window Size

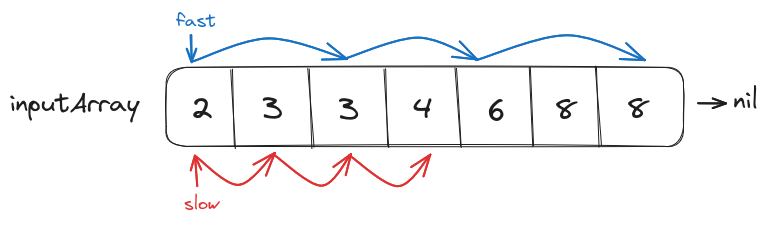
Finding the largest/smallest subsequence satisfying a particular condition inside an array or string requires us to work with an unknown window size. In such cases, to apply the sliding window approach we have to maintain a start and an end pointer, updated dynamically while iterating over the data structure.

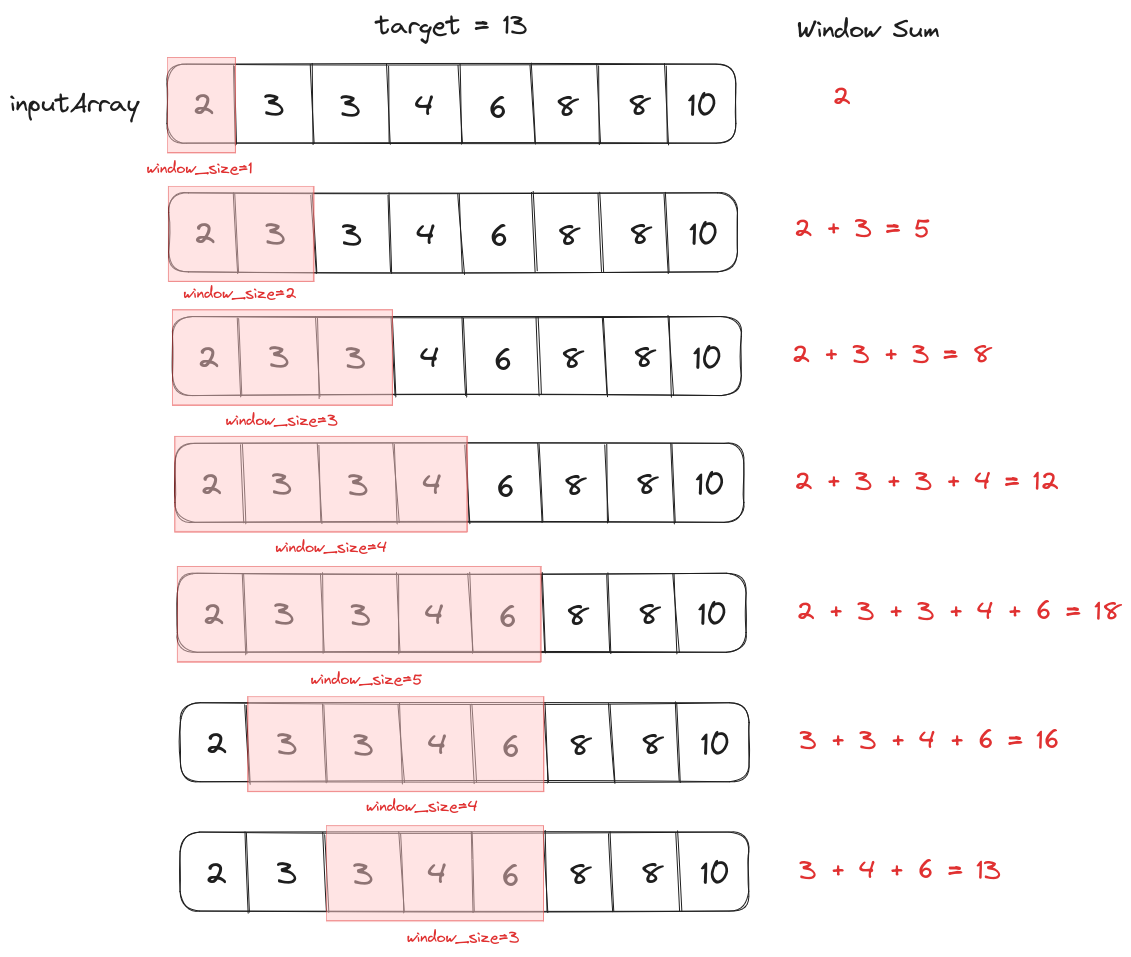
Finding the sub-array that sum up to a target value

Given a sorted array of positive integers as input, we have to find the first sub-array that sums up to a target value.

Since the length of the sub-array is unknown we have to create a dynamically sized window and calculate the sum of its elements. If the sum is smaller than the target value then we will increase the window size from the end and if the window sum is larger than the target value then we decrease its size from the beginning. This cycle will be repeated until we have found the sub-array.

func calculate_sum(array, start, end)
  sum = 0
  for index in [start, end]
    sum += array[index]
  return sum

func find_subarray(array, target)
  start = 0 
  end = 0
  while(end<len(array))
    window_sum = calculate_sum(array, start, end)
    if window_sum < target:

      // If the sum of the current window
      // is smaller than the target value
      // then increase the window size from 
      // the end
      end += 1
    else if window_sum > target:

      // If the sum of the current window
      // is larger than the target value
      // then decrease the window size from 
      // the start
      start += 1
    else:
      return start, end

  return nil, nil

Resources

Two Pointers
Sliding Window
Moving Average
Solve subarray problems FASTER (using Sliding Windows)