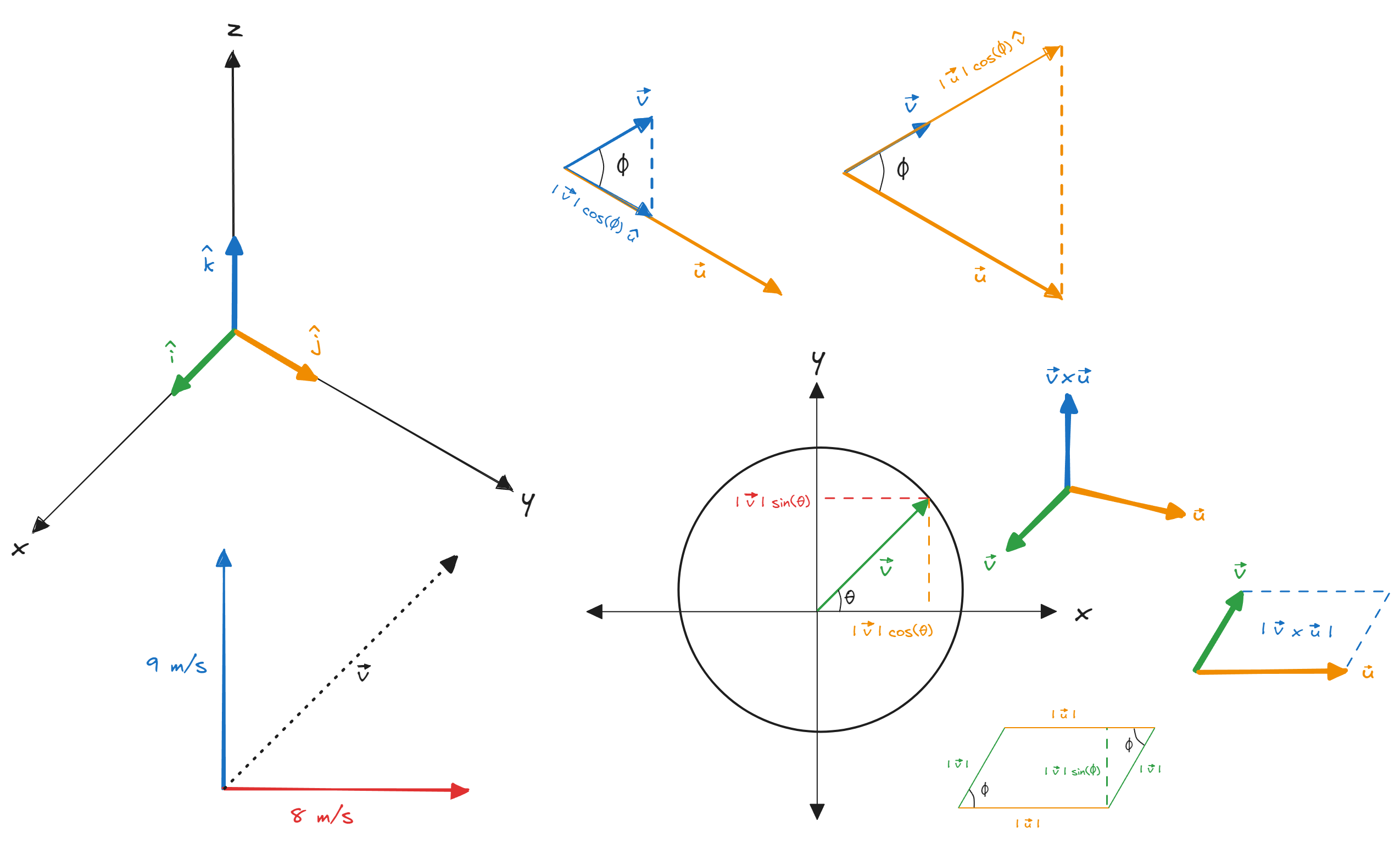
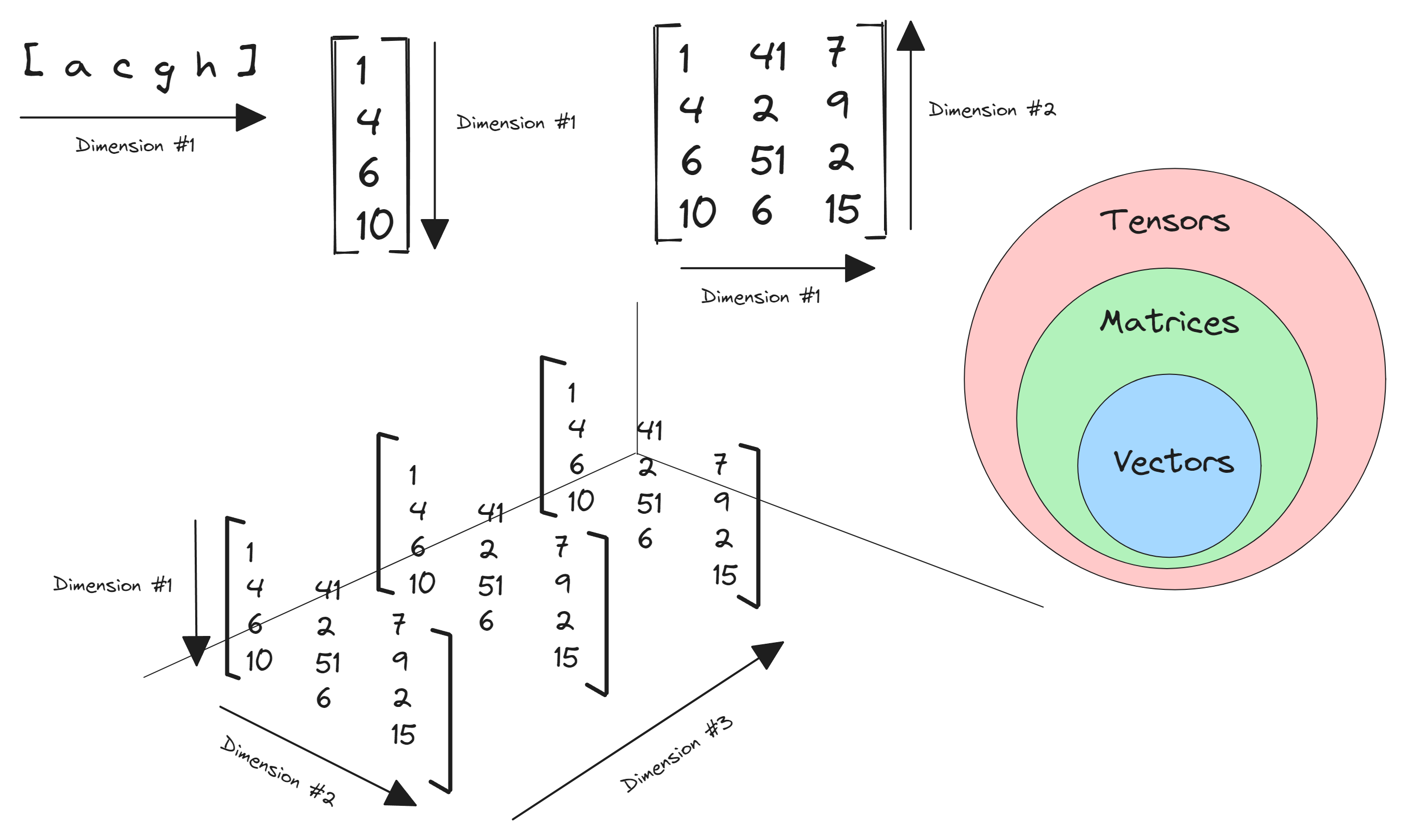
Gaussian Elimination
Let’s consider a problem where we have to buy oranges and apples but under the following conditions. The difference between 2X the number of oranges and the number of apples should be 3. The sum of 4X the number of oranges and the number of apples should be 9. The difference between 5X the number of oranges and 3X the number of apples should be 7. System of Linear Equations These conditions could be modeled using the following equations...